Feval: Parsing a functional language with Parsec

How to use Parsec to parse a functional programming language

In the following we will discuss how to parse the grammar

x ::= ( a | b | ... | z )
      ( a | b | ... | z
      | A | B | ... | Z
      | 0 | 1 | ... | 9
      | _ | ' )*

v ::=   x
      | True | False
      | 0 | 1 | -1 | 2 | -2 | ...
      | Function x -> e
      | [] | [v, v, ..., v]

e ::=   v
      | (e)
      | e && e | e "||" e | !e
      | e + e | e - e | e * e | e / e | e % e
      | e = e | e < e | e <= e | e > e | e >= e
      | e e     -- Function application
      | If e Then e Else e
      | Let x x ... x = e In e
      | e; e
      | e : e | Case e Of [] -> e "|" (x : x) -> e

used for the programming language Feval by utilizing the Parsec library for Haskell. We will find that the daunting task of parsing is made relatively simple with parser combinators.

Basic Background

Parsing is primarily concerned with deriving meaning from strings, i.e. sequences of characters. In the domain of programming languages, this means that we want to read in a string (usually read from a file) that contains a program and convert it to something the interpreter can evaluate. For instance if we have the code 1 - 2 + 3 we would want to be able to convert it to its abstract syntax tree or AST which looks like

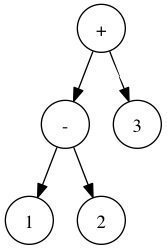
The AST tells the program how to execute the code, which it does in a post-order traversal, i.e. it evaluates the right and left children before the parent. The way that we represent the AST in Haskell is by defining a grammar for our language, and then an actual type. For the expression above we could define the grammar for our language to be

v ::= 1 | -1 | 2 | -2 | 3 | -3 | ...

e ::= e + e | e - e | v

In this case our values denoted by the variable v can be any integer, whereas our expressions, denoted by the variable e, can only be addition of any two expressions, subtraction of any two expressions, or any value. We can represent this grammar in type form as follows

data Expr =
       Add Expr Expr
     | Sub Expr Expr
     | Num Integer
     deriving Show

Usually when you have to do something with parsing you have a whole lot of baggage that comes along with it. Things like whitespace, the state of the parser (what line you are on, etc.), or even what to do when there is a syntax error on the part of the programmer, can be a lot to handle and annoying to have to deal with. Fortunately Parsec makes all this easy.

Parse on, Captain

First off, to deal with whitespace all we need to do is create a lexer, which takes our program and returns tokens, things like "45", "-12", "+", or "-" while removing whitespace. First we define the configuration for our lexer

import Text.Parsec hiding (Empty)
import Text.Parsec.String
import qualified Text.Parsec.Token as Token
import Text.Parsec.Language

lexerConfig = emptyDef { Token.reservedOpNames = words "+ -" }

This lexer config says that the symbols "+" and "-" are reserved operators. Then we create our lexer and extract some useful functions from it

lexer = Token.makeTokenParser lexerConfig

reservedOp = Token.reservedOp lexer
integer    = Token.integer lexer

Now we can get down to the gritty details. The Parsec parser is a monad that abstracts everything but the results of successful parsing away from us so that we don't have to deal with it. Because of the monad structure, we are easily able to combine smaller parsers together to form a larger parser. In this way we will find that our parser resembles its original grammar.

Lets first start our with our parser for a value. The only type of value we can have is an integer so therefore, our parser can be written

value :: Parser Expr
value = do
    n <- integer
    return $ Num n

The integer parser returns an integer monadically, which we extract to form a value Expr, namely an instance of Num Integer. In the case that the integer fails, i.e. cannot parse an input, the value parser will fail without consuming any input.

(It is important to note that this would not be the case if the value parser were made to consume something else before the integer, for instance Integer before an expression like Integer -78. In this case after consuming a string containing "Integer", if the integer parser were to fail, the "Integer" would still be consumed by the value parser even if it fails. If you need to fail without consuming input in this type of scenario you should wrap your parser inside of Parsec's try function.)

Now we need to parse expressions, specifically our expressions involving the operators + and -. In most cases this type of parsing is hard and annoying, if not downright impossible, but fortunately Parsec comes to the rescue once again! First we define a function which will construct a configuration that tells Parsec's expression library how to parse our expression

import Text.Parsec.Expr

binary name label assoc = Infix (do{ reservedOp name
                                   ; return (\x y -> label x y)
                                   }) assoc

This tells the expression parser that we are creating an infix operator with an associativity assoc and a parser for the operator, which must return a function to construct the expression parsers return type. In this case the parser parses one of our reserved operators name and returns the label type with the left and right parts of the expression applied to x and y. We can then define an operator table

opTable = [ [ binary "+" Add AssocLeft
            , binary "-" Sub AssocLeft ] ]

which says that both addition and subtraction are binary operations that associate left with names + and -, and types Add and Sub, respectively. Then our expression parser is

expr :: Parser Expr
expr = buildExpressionParser opTable value

which says that the parser for the right and left of an expression is either a value or another expression from the opTable.

Great, but how do I use it? You can easily parse both strings and files via

import Control.Applicative ((<*))

parseString :: Parser Expr -> String -> Either ParseError Expr
parseString e s = parse (e <* eof) "" s

parseFile :: Parser Expr -> FilePath -> IO (Either ParseError Expr)
parseFile e f = parseFromFile (e <* eof) f

Here, the eof is a parser which parses the end of a string or file, and the (<*) operator, which we can use since the Parsers are monads, which evaluates both parsers but returns only the result from the one on the left. ParseError simply contains information about what happened in the case of a parsing failure. Conveniently, it is an instance of Show.

Data Aquisition

In feval we can convert our grammar to a data type like so

data Expr
    = CInt Integer
    | CBool Bool
    | CVar String
    | Add Expr Expr
    | Sub Expr Expr
    | Mul Expr Expr
    | Div Expr Expr
    | Mod Expr Expr
    | And Expr Expr
    | Or Expr Expr
    | Not Expr
    | Equal Expr Expr
    | Less Expr Expr
    | LessEq Expr Expr
    | Great Expr Expr
    | GreatEq Expr Expr
    | Empty -- []
    | Cons Expr Expr
    | If Expr Expr Expr
    | Function String Expr
    | Appl Expr Expr
    | Let String [String] Expr Expr -- Let String String String ... = Expr In Expr
    | Semi Expr Expr -- Expr; Expr
    | Case Expr Expr String String Expr -- Case Expr Of [] -> Expr | (String, String) -> Expr
    deriving Show

To correspond with our grammar, we define the following lexer

names = words "True False Function If Then Else Let In Case Of" -- reserved names
opNames = words "-> && || ! + - * / % = ; < <= > >= :" -- reserved operations

lexerConfig = emptyDef { Token.commentStart = "/*" -- adding comments is easy
                       , Token.commentEnd = "*/"
                       , Token.commentLine = "#"
                       , Token.identStart = letter -- identifiers must start with a letter
                       , Token.identLetter = alphaNum <|> char '_' <|> char '\''
                       , Token.reservedNames = names
                       , Token.reservedOpNames = opNames
                       }

lexer = Token.makeTokenParser lexerConfig

The letter parser is a parser that parses any letter. The alphaNum parses any letter or number character. The char parser parses only it's character argument. The (<|>) operation runs the left-most parser and then the next until one succeeds; if all fail so does the overall parser. We export the following functions from the lexer

identifier = Token.identifier lexer -- parses a valid identifier in our language
symbol     = Token.symbol lexer     -- parses a symbol like "]"
reserved   = Token.reserved lexer   -- parses a reserved word like "If"
reservedOp = Token.reservedOp lexer -- parses a reserved operation like "<="
parens     = Token.parens lexer     -- parses parenthesis surrounding the parser passed to it
brackets   = Token.brackets lexer   -- parses brackets surrounding the parser passed to it
commaSep   = Token.commaSep lexer   -- parses some or no comma separated instances of
                                    -- the argument parser
integer    = Token.integer lexer    -- parses an integer
whiteSpace = Token.whiteSpace lexer -- parses whitespace

Expressions and an `Appl`

We next move on to our easiest parser, the operation expression parser (who would have thought...). All we need to do is to define a prefix function to complement our binary function described earlier

import Control.Applicative ((*>)) -- the opposite of (<*)

prefix name label = Prefix (reservedOp name *> return (\x -> label x))

And we can define a ton of expressions quite easily

opTable = [ [ prefix "!" Not ]
          , [ appl ]
          , [ binary "*" Mul AssocLeft
            , binary "/" Div AssocLeft
            , binary "%" Mod AssocLeft ]
          , [ binary "+" Add AssocLeft
            , binary "-" Sub AssocLeft
            ]
          , [ binary "=" Equal AssocLeft
            , binary "<" Less AssocLeft
            , binary "<=" LessEq AssocLeft
            , binary ">" Great AssocLeft
            , binary ">=" GreatEq AssocLeft
            ]
          , [ binary "&&" And AssocLeft ]
          , [ binary "||" Or AssocLeft ]
          , [ binary ":" Cons AssocRight ]
          , [ binary ";" Semi AssocLeft ]
          ]

Note that the operation lists at the top have the highest precedence (operations in the same list have the same precedence). But what is this appl in our tree (haha)? This is our operation for function application, which uses spaces between arguments instead of an operator, for example an expression like (Function x -> x + 1) 3. We need to be careful with how we define application, because there is usually a space between the operators and arguments in other expressions. Therefore, we define appl as

appl = Infix space AssocLeft
    where space = whiteSpace
            *> notFollowedBy (choice . map reservedOp $ opNames)
            *> return (\x y -> Appl x y)

The appl parser first consumes any whitespace, then it makes sure that it is not followed by an operation. We do this by taking the array of operator names and mapping the reserved operation parser function reservedOp over it. We then wrap this into a choice parser which parses at least one of the parsers in the list passed to it as an argument. Then we apply this to the parser notFollowedBy, which does not fail only if the next string (looking ahead) cannot be parsed by its argument.

Finally, we can define our operator expression parser as

opExpr :: Parser Expr
opExpr = buildExpressionParser opTable term

Terms of Service

First we define parsers for our basic constant types

import Control.Applicative ( (<$>)  -- This takes an argument on its right,
                                    -- in this case the value inside the
                                    -- monadic parser, and applies it to the function to
                                    -- the left (if the parser does not fail)
                           , (<$) ) -- This takes an monadic parser on its right
                                    -- and returns the value on the left (if the
                                    -- parser does not fail)

cint :: Parser Expr
cint = CInt <$> integer

cbool :: Parser Expr
cbool = CBool True <$ reserved "True"
    <|> CBool False <$ reserved "False"

cvar :: Parser Expr
cvar = CVar <$> identifier

Next we define our list parser

list :: Parser Expr
list = toCons <$> brackets (commaSep expr)
    where toCons [] = Empty
          toCons (x:xs) = Cons x (toCons xs)

This parser reads in some or no expr parsers separated by commas and encapsulated with brackets, and applies the resulting list to the toCons function before returning it monadically.

At last we can define the term parser that we used in our opExpr parser

term :: Parser Expr
term =  cint
    <|> cbool
    <|> cvar
    <|> list
    <|> parens expr -- parentheses surrounded expression

`Let`'s, `Case`'s, `Function`'s, and `If`'s

Now that we have our basic building blocks defining more complicated expressions is just a matter of combining them in the right way. We define our Let to be

letExpr :: Parser Expr
letExpr = reserved "Let" *> do -- parse the reserved word Let; return the do block
    s <- sepBy1 identifier whiteSpace
    reservedOp "="
    e <- expr
    reserved "In"
    e' <- expr
    case s of (x:xs) -> return $ Let x xs e e' -- we must have at least one

The sepBy1 parser parses one or more instances of the parser passed as its first argument, separated by one instance each of the parsers passed as its argument. Note that we need to have at least one identifier to be the name of the variable being defined. The rest of the do block just parses the rest of the expression before returning the result.

Our Case parser is

caseExpr :: Parser Expr
caseExpr = reserved "Case" *> do
    p <- expr
    reserved "Of" *> symbol "[]" *> reservedOp "->" -- parse an "Of", a "[]", then a "->"
    x <- expr
    reservedOp "|"
    (s, t) <- parens $ do{ s' <- identifier -- return the do block within parentheses
                         ; reservedOp ":"
                         ; t' <- identifier
                         ; return (s', t')
                         }
    reservedOp "->"
    y <- expr
    return $ Case p x s t y

Define our Function parser to be

import Control.Applicative ((<*>)) -- Adds an extra argument to (<$>)

function :: Parser Expr
function = reserved "Function" *> ((\x y -> Function x y)
    <$> identifier <*> (reservedOp "->" *> expr)

which parses the reserved word Function, then an identifier, a reserved operation ->, and an expression, and returns the Expr monadically.

Our If parser is then simply

ifExpr :: Parser Expr
ifExpr = reserved "If" *> ((\x y z -> If x y z)
    <$> expr <*> (reserved "Then" *> expr) <*> (reserved "Else" *> expr))

Finally, we can define our Expr parser

expr :: Parser Expr
expr =  function
    <|> letExpr
    <|> ifExpr
    <|> caseExpr
    <|> opExpr
    <|> term

Wait... are we? Yes, that is right. This is the entire parser. Just fire up our parseString and parseFile functions and test it out.

Afterword

Hopefully the preceding discussion has helped you learn how you can use Parsec. The parser we created is nearly verbatim what I wrote for Feval, except instead of a simple type Expr, I use the type Expr a since I want the type to be a functor, which I make recursive with the type Fix

data Expr a = Num Integer | ...

newtype Fix f = Fx (f (Fix f))

type NewExpr = Fix Expr

(More information on this in this article.)

Happy parsing!